La Geometría molecular o estructura molecular se refiere a la disposición tri-dimensional de los átomos que constituyen una molécula. Determina muchas de las propiedades de las moléculas, como son la reactividad, polaridad, fase, color, magnetismo, actividad biológica, etc.
Geometria molecular
Dado que el movimiento de los átomos en una molécula está determinado por la mecánica cuántica, uno debe definir el "movimiento" de una manera cuántica.
Los movimientos cuánticos (externos) de traslación y rotación cambian fuertemente la geometría molecular. (En algún grado la rotación influye en la geometría por medio de la fuerza de Coriolis y la distorsión centrífuga, pero son despreciables en la presente discusión).
Un tercer tipo de movimiento es la vibración, un movimiento interno de los átomos en una molécula. Las vibraciones moleculares son armónicas (al menos en una primera aproximación), lo que significa que los átomos oscilan en torno a su posición de equilibrio, incluso a la temperatura del cero absoluto. En el cero absoluto todos los átomos están en su estado vibracional basal y muestran movimiento mecánico cuántico de punto cero, esto es, la función de onda de un modo vibracional simple no es un pico agudo, sino un exponencial de ancho finito. A temperaturas mayores, los modos vibracionales pueden ser excitados térmicamente (en un interpretación clásica, esto se expresa al enunciar que "las moléculas vibrarán más rápido"), pero siempre oscilan alrededor de una geometría reconocible para la molécula.
Para tener una comprensión más clara de la probabilidad de que la vibración de una molécula pueda ser térmicamente excitada, se inspecciona el factor de Boltzmann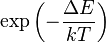 
, donde ΔEes la energía de excitación del modo vibracional, k es la constante de Boltzmann y T es la temperatura absoluta. A 298K (25 °C), unos valores típicos del factor de Boltzmann son: ΔE = 500 cm-1 --> 0.089; ΔE = 1000 cm-1 --> 0.008; ΔE = 1500 cm-1 --> 7 10-4. Esto es, si la energía de excitación es 500 cm-1, aproximadamente el 9% de las moléculas están térmicamente excitadas a temperatura ambiente. La menor energía vibracional de excitación es el modo de flexión (aproximadamente 1600 cm-1). En consecuencia, a temperatura ambiente menos del 0,07% de todas las moléculas de una cantidad dada de agua vibrarán más rápido que en el cero absoluto.
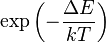, donde ΔEes la energía de excitación del modo vibracional, k es la constante de Boltzmann y T es la temperatura absoluta. A 298K (25 °C), unos valores típicos del factor de Boltzmann son: ΔE = 500 cm-1 --> 0.089; ΔE = 1000 cm-1 --> 0.008; ΔE = 1500 cm-1 --> 7 10-4. Esto es, si la energía de excitación es 500 cm-1, aproximadamente el 9% de las moléculas están térmicamente excitadas a temperatura ambiente. La menor energía vibracional de excitación es el modo de flexión (aproximadamente 1600 cm-1). En consecuencia, a temperatura ambiente menos del 0,07% de todas las moléculas de una cantidad dada de agua vibrarán más rápido que en el cero absoluto.Como se mencionó anteriormente, la rotación influye fuertemente sobre la geometría molecular. Pero, como movimiento mecánico cuántico, se excita a bajas temperaturas (comparada con la vibración). Desde un punto de vista clásico, puede decirse que más moléculas rotan más rápidamente a temperatura ambiente, esto es que tienen mayor velocidad angular y momentum angular. En lenguaje de mecánica cuántica: más "eigenstates" de alto momentum angular son poblados térmicamente al aumentar la temperatura. Las energías de excitación rotacionales típicas están en el orden de unos pocos cm-1.
Los resultados de muchos experimentos espectroscópicos están ensanchados porque involucran una media de varios estados rotacionales. Frecuentemente es difícil obtener las geometrías a partir de los espectros a altas temperaturas, porque el número de estados rotacionales rastreados en el experimento aumenta al incrementarse la temperatura. En consecuencia, muchas observaciones espectroscópicas sólo se puede esperar que conduzcan a geometrías moleculares confiables a temperaturas cercanas al cero absoluto.
Tipos de estructura molecular
Pares de Electrones Compartidos | Pares de Electrones Solitarios | Distribución | Geometría | Ángulo de Enlace Ideal | Ejemplo | Imagen |
|---|---|---|---|---|---|---|
 | ||||||
 | ||||||
 | ||||||
 | ||||||
 | ||||||
 | ||||||
 | ||||||
 | ||||||
 | ||||||
 | ||||||
 | ||||||
 | ||||||
 |
Luis Sanguinetti
4to "C" nº:32
No hay comentarios:
Publicar un comentario