Los materigillos: Lo basico para aprobar sobre poliedros

Concepto:

Un poliedro es, en el sentido dado por la geometria clásica al término, un cuerpo geométrico cuyas caras son planas y encierran un volumen finito. La palabra poliedro viene del griego clásico de la palabra πολύεδρον, de poli-muchas y edron-caras.

Los poliedros son denominados de acuerdo a su número de caras. El sistema de denominación se basa de nuevo en el griego clásico.

A diferencia de los poliedros comunes estos tiene angulos, lados y caras iguales.

Según Platón el universo se formaba por 5 poliedros regulares:

Tetraedro

Su superficie está formada por 4 triángulos equiláteros iguales.

Tiene cuatro vértices y cuatro aristas.

Es una pirámide triangular regular.

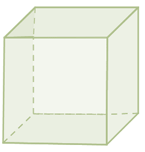
Hexaedro o cubo

Su superficie está constituida por 6 cuadrados..

Tiene 8 vértices y 12 aristas..

Es un prisma cuadrangular regular. .

Octaedro

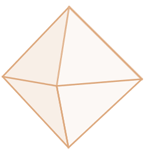
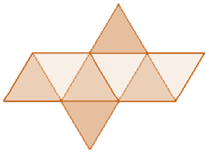
Su superficie consta de ocho triángulos equiláteros.

Tiene 6 vértices y 12 aristas.

Se puede considerar formado por la unión, desde sus bases, de dos pirámides cuadrangulares regulares iguales.

Dodecaedro

Su superficie consta de 12 pentágonos regulares.

Tiene 20 vértices y 30 aristas.

Icosaedro

Su superficie consta de veinte triángulos equiláteros.

Tiene 12 vértices y 30 aristas.

En la antiguedad tambien se usaron para representar los elementos:

Si, pero se les conoce mejor como poliedros regulares cóncavos, conocidos como Sólidos de Kepler-Poinsot:

Un sólido de Kepler (también llamado sólido de Kepler-Poinsot) es un poliedro regular no convexo, cuyas caras son todas polígonos regulares y que tiene en todos sus vértices el mismo número de caras que se encuentran (compárese con los sólidos platónicos).

Las caras están solo parcialmente en la superficie del sólido, y las partes expuestas están sólo conectadas en puntos (si están conectadas de algún modo). Si las partes se cuentan como caras separadas, el sólido deja de ser regular.

Un sólido de Kepler cubre su esfera circunscrita más de una vez, con los centros de las caras como puntos direccionales en los sólidos con caras en forma de pentagrama, mientras que en los otros son los vértices los que cumplen esa función. Por esta razón, no son necesariamente equivalentes topológicos de la esfera como lo son los sólidos platónicos, y en particular la característica de Euler V − E + F = 2 se verifica solamente para Gran dodecaedro estrellado y Gran icosaedro.

Esto dependerá de cómo observemos el poliedro. Considérese, por ejemplo, el pequeño dodecaedro estrellado. Consiste de un dodecaedro con una pirámide pentagonal en cada una de sus 12 caras. En consecuencia, las 12 caras se extienden a pentagramas con el pentágono central dentro del sólido. La parte externa de cada cara consiste de cinco triángulos conectados por sólo cinco puntos. Si las contamos separadamente, hay 60 caras (pero estas son triángulos isósceles, no polígonos regulares). De modo similar, cada lado puede ser contado como tres, pero entonces los habrá de dos tipos. Igualmente, con los “cinco puntos” antes mencionados: en total habrá 20 puntos que pueden contarse como vértices, por lo que tendremos un total de 32 vértices (otra vez, de dos tipos). Ahora la ecuación de Euler se verifica: 60 – 90 + 32 = 2.