El Teorema de Pitágoras establece que en un triángulo rectángulo el cuadrado de la longitud de la hipotenusa es igual a la suma de los cuadrados de las longitudes de los dos catetos. Si un triángulo rectángulo tiene catetos de longitudes  y
y  , y la medida de la hipotenusa es
, y la medida de la hipotenusa es  , se establece que:
, se establece que:
 y
y  , y la medida de la hipotenusa es
, y la medida de la hipotenusa es  , se establece que:
, se establece que:Un poco de la historia de este teorema--------->El Teorema de Pitágoras
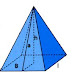
 lleva este nombre porque su descubrimiento sobre la escuela pitagórica. Anteriormente, en Mesopotamia y el Antiguo Egipto se conocían ternas de valores que se correspondían con los lados de un triángulo rectángulo, y se utilizaban para resolver problemas referentes a los triángulos rectangulos, tal como se indica en algunas tablillas y papiros, pero no ha perdurado ningún documento que exponga teóricamente su relación. La pirámide de Kefrén, datada en el siglo XXVI a. C., fue la primera gran pirámide que se construyó basándose en el llamado triángulo sagrado egipcio, de proporciones 3-4-5.
lleva este nombre porque su descubrimiento sobre la escuela pitagórica. Anteriormente, en Mesopotamia y el Antiguo Egipto se conocían ternas de valores que se correspondían con los lados de un triángulo rectángulo, y se utilizaban para resolver problemas referentes a los triángulos rectangulos, tal como se indica en algunas tablillas y papiros, pero no ha perdurado ningún documento que exponga teóricamente su relación. La pirámide de Kefrén, datada en el siglo XXVI a. C., fue la primera gran pirámide que se construyó basándose en el llamado triángulo sagrado egipcio, de proporciones 3-4-5.- Demostración :
 .
.Es evidente que el área del cuadrado de lado c es la suma del área de los cuatro triángulos de altura a y base b que están dentro de él más el área del cuadrado menor:
Publicado Por : Juan Diego Urbano Flores 4to C


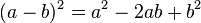
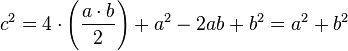
No hay comentarios:
Publicar un comentario